Интегрировать и «Фурьировать» можно конечно, и мощность и импеданс, в случае если сигнал достаточно предсказуемый – к примеру, розовый и белый шум (хотя бы зная некоторые его параметры – диапазон частот в котором находится спектр, АЧХ, средние и пиковые амплитуды напряжения). Кстати, тема то достаточно серьёзная и имеет большое значение для практического применения. Когда работаешь с синусоидальными сигналами, хули, конечно…, всё просто… и токи, и напряжения, и количество тепла, выделяемое в нагрузке можно очень просто вычислить. Вот с тем, что импеданс (снятый на синусоидальном сигнале) не может падать ниже активного – с этим я согласен, абсолютно  ! Действительно, в этом случае, реактивное сопротивление катушки всегда включено последовательно активным, и «упасть» ниже оного не может. ! Действительно, в этом случае, реактивное сопротивление катушки всегда включено последовательно активным, и «упасть» ниже оного не может.
Но в реальной радиотехнике, работа с чисто гармоническими колебаниями является исключительно редким случаем, обычно, по мимо синуса в сигналах полным-полно всякой хуйни. Скажем, в ключевых схемах, тех же полумостах и речи о синусе не идёт. Мне лично, это нужно несколько для другой области техники (а по большому счету, какая разница). В паспортах на акустические системы всегда (ещё раз подчеркну – всегда) приводится график импеданса при изменении частоты сигнала. Да отлично! Берём синус с желаемой частотой, подаём на колонку, затем, по графику импеданса (на эту колонку) находим оный, считаем потребляемую мощность и тепло выделяемое в звуковой катушке. Заибись, охуительно! Но где Вы (мы, я) видели, что бы, на акустическую систему подавали чистый синус… Да нет такого! Туда валят, всё что не попадя – музыку, речь, всякую херь :-| o_O , с очень сложной, не предсказуемой природой. Следовательно, четко знать параметры нагрузки для данных видов сигнала не представляется возможным, тем более для этого применять вышеупомянутый график.
В результате, не представляя, каковы параметры нагрузки для конкретного электрического сигнала, мы не можем точно рассчитать потребляемую мощность и самое главное тепловой режим. После этого, всё завалено жжеными фетами и динамиками.
У меня конкретно, очень большая нехватка литературы в этой области. Если у кого есть какие-то зцылки по проблеме, типа «мощность спектра электрических сигналов», или тому подобное, то я был бы очень благодарен, заранее..
На данный момент, я считаю (благодаря проведённым мной расчетам), что суммарный импеданс индуктивной нагрузки (для сигналов имеющих сложный спектр) находится ниже, чем её активное сопротивление. Но я могу ошибаться, но при этом хочу лично убедиться, в том что я ошибаюсь.
Добавлено: Tue Dec 04, 2007 11:52 am
|
 ! Действительно, в этом случае, реактивное сопротивление катушки всегда включено последовательно активным, и «упасть» ниже оного не может.
! Действительно, в этом случае, реактивное сопротивление катушки всегда включено последовательно активным, и «упасть» ниже оного не может.
 ) Нужно?
) Нужно?

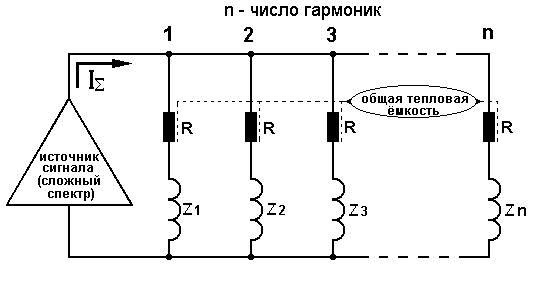
 , особенно нужно выяснить можно ли вообще при несинусоидальном «широкополосном» сигнале рассчитывать комплексный импеданс. Может этого вообще делать нельзя. Если ниже приведённые формулы не правильны, их нужно исправить.
, особенно нужно выяснить можно ли вообще при несинусоидальном «широкополосном» сигнале рассчитывать комплексный импеданс. Может этого вообще делать нельзя. Если ниже приведённые формулы не правильны, их нужно исправить.

